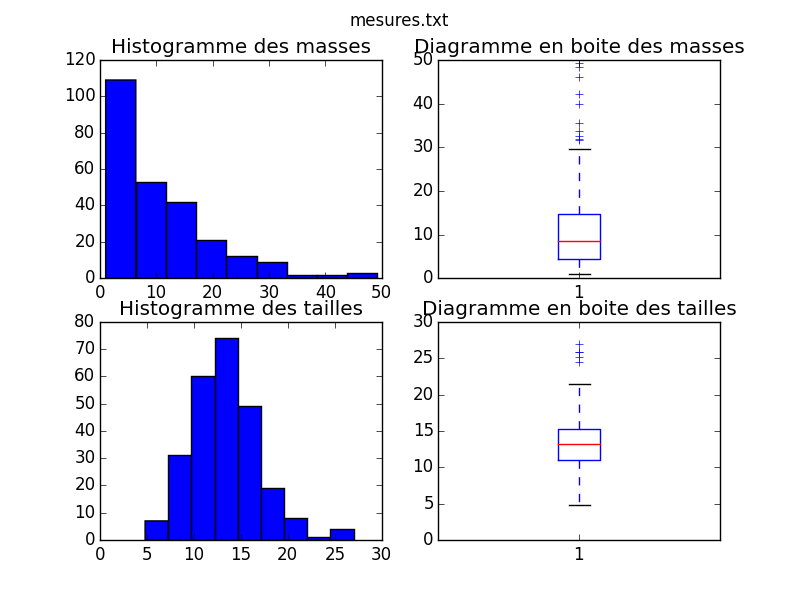
Diagramme
852 - M.Lalauze - M.Junier
On appellera cette fonction sur le fichier mesures.txt sans la ligne indiquant les moyennes !
import matplotlib.pyplot as plt
from math import log,ceil,sqrt
import numpy as np
def diagramme(fichier):
masse,taille = lecture(fichier)
#longueur de la série
n = len(masse)
plt.suptitle(fichier)
plt.subplot(221)
plt.title('Histogramme des masses')
#nb de classes = sup(log(n,2)+1) calculé d'après la regle de Sturges
nclasses = ceil(log(n,2)+1)
plt.hist(masse,bins=nclasses)
plt.subplot(222)
plt.title('Diagramme en boite des masses')
plt.boxplot(masse)
plt.subplot(223)
plt.title('Histogramme des tailles')
plt.hist(taille,bins=nclasses)
plt.subplot(224)
plt.title('Diagramme en boite des tailles')
plt.boxplot(taille)
plt.savefig('Diagrammes-{}.png'.format(fichier.rstrip('.txt')))
plt.show()
Diagramme
lauriers = open('mesures_lauriers.txt','r')
masse = 0
taille = 0
nb_lauriers = 0
for ligne in lauriers:
liste=ligne.strip().split('\t')
nb_lauriers += 1
masse += float(liste[0])
taille += float(liste[1])
print('la masse moyenne des lauriers roses est de {:.2f} et leur taille moyenne de {:.2f}'.format(masse/nb_lauriers, taille/nb_lauriers))
lauriers.close()
def bilan_regression(fichier):
'''La procédure récupère d'abord les listes dans fichier deux listes x et y de flottants de même longueur.
La procédure calcule les listes x2,y2 et xy respectivement des carrés et des produits terme à terme des éléments de x et de y.
Puis elle calcule la covariance les variances v(x) et v(y), la covariance cov(x,y), le coefficient de corrélation linéaire r(x,y), l'équation de la droite de régression de y en x.
Elle recopie x,y,x2,y2 et xy en colonnes séparées par des virgules
Elle recopie les valeurs sum(x),sum(y),sum(x2),sum(y2),sum(xy) ligne par ligne dans un fichier regression.txt.
On complète ce fichier avec la moyenne en x, la moyenne en y, les écarts types en x et y, la cov(x,y), le coefficient de corrélation linéaire, et l'équation de la droite de régression.
Puis elle affiche un graphique avec le nuage de points (x,y) et la droite de régression de y en x.
'''
x,y = lecture(fichier)
# utilisation de listes en compréhensions
n = len(x)
#carrés de x
x2 = [i**2 for i in x]
#carrés de y
y2 = [j**2 for j in y]
#moyenne de x
mx = sum(x)/n
#moyenne de y
my = sum(y)/n
#variance de x
vx = sum(x2)/n-(mx)**2
#variance de y
vy = sum(y2)/n-(my)**2
#xy = [i*j for i,j in zip(x,y)]
xy = [x[i]*y[i] for i in range(n)]
#covariance de x et y
covxy = sum(xy)/n-mx*my
#coefficient de corrélation linéaire
rxy = covxy/sqrt(vx*vy)
#coefficient directeur a de la droite de régression de y en x
a = covxy/vx
#ordonnée à l'origie de la droite de régression de y en x
b = my-a*mx
# Ecriture dans le fichier regression.csv
f = open('regression.txt','w')
f.write('Totaux\n')
f.write('sum(x) : {:.2f}, sum(y) : {:.2f}, sum(x^2) : {:.2f}, sum(y^2) : {:.2f}, sum(xy) : {:.2f}\n'.format(sum(x),sum(y),sum(x2),sum(y2),sum(xy)))
f.write('Moyennes\n')
f.write('moyenne x : {:.2f},moyenne y {:.2f}\n'.format(mx,my))
f.write('Ecarts-types\n')
f.write('sigma x : {:.2f}, sigma y : {:.2f}\n'.format(sqrt(vx),sqrt(vy)))
f.write('Covariance de x et de y : {:.2f}\n'.format(covxy))
f.write('Coefficient de corrélation linéaire de x et y : {:.2f}\n'.format(rxy))
f.write('Equation de la droite de régression de y en x : y={:.2f}x+{:.2f}'.format(a,b))
f.close()
# Affichage du graphique
t = np.linspace(min(x),5/4*max(x)-1/4*min(x),1000)
#fonction affine de la droite de régression de y en x
#g = lambda u:a*u+b
#z = g(t)
z = [a*t[i]+b for i in range(len(t))]
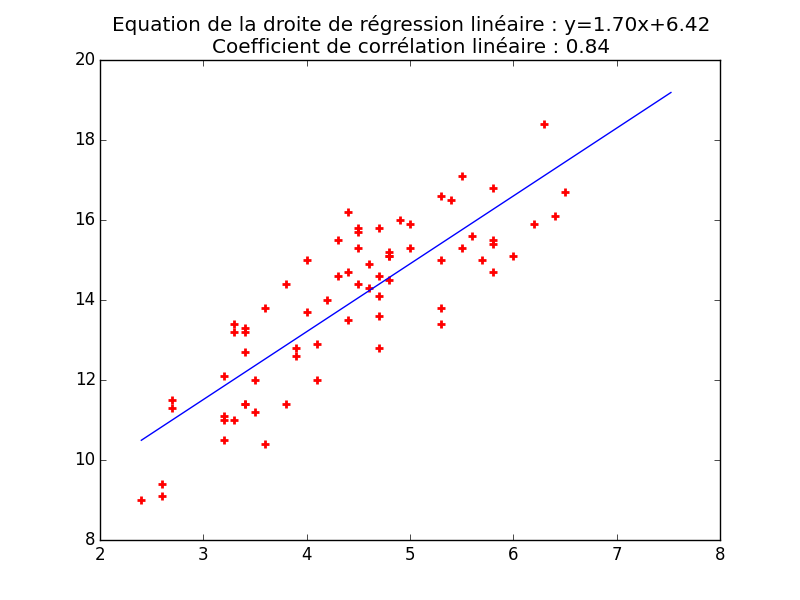
plt.title('Equation de la droite de régression linéaire : y={:.2f}x+{:.2f}\nCoefficient de corrélation linéaire : {:.2f}'.format(a,b,rxy))
plt.plot(x,y,'r+',markeredgewidth=2)
plt.plot(t,z,'b-')
plt.savefig('regression.png')
plt.show()
"""
Totaux
sum(x) : 312.80, sum(y) : 986.60, sum(x^2) : 1451.04, sum(y^2) : 14006.96, sum(xy) : 4470.36
Moyennes
moyenne x : 4.41,moyenne y 13.90
Ecarts-types
sigma x : 1.01, sigma y : 2.05
Covariance de x et de y : 1.74
Coefficient de corrélation linéaire de x et y : 0.84
Equation de la droite de régression de y en x : y=1.70x+6.42
"""
Régression linéaire
def recherche_fasta(fichier,mot,encodage='utf8'):
'''recherche la première occurence d'un mot dans une séquence de genes ou d'acides aminés contenue dans un fichier texte au format fasta.
Pour plus d'infos sur le format fasta voir http://fr.wikipedia.org/wiki/FASTA_%28format_de_fichier%29.
On ne traite pas le cas des mots coupés en fin de ligne.'''
f = open(fichier,'r',encoding=encodage)
texte = f.read()
ltexte = len(texte) #longueur du texte
lmot = len(mot) #longueur du mot
i = 0
while i < ltexte - lmot + 1:
j = 0
while j < lmot and texte[ i + j ] == mot[ j ]:
j += 1
if j == len(mot):
return i
i += 1
f.close()
return None
fichier = 'exemple_fasta.txt'
mot = 'TCACGG'
res =recherche_fasta(fichier,mot)
if res:
print("La première occurence du mot {} est en position {} dans le fichier {}".format(mot,res,fichier))
f = open(fichier,'r')
texte = f.read()
l = len(mot)
print(texte[res:res+l])
f.close()
else:
print("Le mot {} n'apparait pas dans le fichier {}".format(mot,fichier))
Documentation de Python pour la manipulation de fichier
Tutoriels sur les bibliothèques Numpy et Matplotlib pour la création de graphiques :