Exercice 2 : Recherche simultanée de maximum et minimum

def maxi(t):
    '''Retourne le maximum d'un tableau d'entiers'''
    n = len(t)
    if len(t) == 0:
        return None
    M = t[0]
    for k in range(1, n):
        element = t[k]
        if element > M:
            M = element
    return M

def mini(t):
    '''Retourne le minimum d'un tableau d'entiers'''
    if len(t) == 0:
        return None
    m = t[0]
    for element in t[1:]:
        if element < m:
            m = element
    return m

def extremum_simultane(L):
    '''Recherche simultane du maximum et du minimum par paire
    Complexité linéaire, n/2 + 2*(n/2 - 1) = 3n/2 - 2 comparaisons'''
    
    def maxmin_paire(a, b):
        if a > b:
            return a, b
        return b, a
    
    taille = len(L)
    #liste vide
    if taille == 0:
        return
    #liste de longueur impaire complété avec le dernier element doublé
    if taille%2 == 1:
        L.append(L[-1])
    #initialisation du maxcourant et du mincourant
    maxcourant, mincourant = maxmin_paire(L[0], L[1])
    for k in range(1, taille//2):
        maxp, minp = maxmin_paire(L[2*k], L[2*k + 1])
        if maxp > maxcourant:
            maxcourant = maxp
        if minp < mincourant:
            mincourant = minp
    return mincourant, maxcourant
    
"""
>>> min_maxi([10,5,18,6])
(5, 18)

>>> min_maxi([10,5,18,6,843,-15,0])
(-15, 843)
"""

Analyse de complexité (en nombre de comparaisons et par rapport à la taille \(n\) du tableau t ) :

Pour les fonctions maxi(t) et mini(t), il faut \(n\) comparaisons si \(n\) est la taille du tableau. Ces fonctions ont donc une complexité de \(n\) donc en \(O(n)\).
Pour la recherche simultanée du minimum et du maximum :
- Deux appels successifs à maxi(t) et mini(t) donnent une complexité de \(2n\) donc en \(O(n)\) mais avec une constante plus grande que la recherche d’un seul extremum.
- Si on rassemble les comparaisons des deux boucles des fonctions dans une même boucle, le nombre de comparaisons de change pas.
- En revanche la fonction min_maxi(t) effectue \(3\) comparaisons par tour de boucles et environ \(\lfloor \frac{n}{2} \rfloor\) tours de boucles soit environ \(\lfloor \frac{3n}{2} \rfloor\) comparaisons. La complexité est en \(O(n)\) mais avec une constante plus petite.

Exercice 3 : Run-length encoding

def compresse(u):
    """le premier élément est égal au premier élément de u (ici 1) ;
 ensuite, on indique le nombre de fois que cet élément est répété (ici 3) ;
 à chaque fois qu’une série se termine, on indique la longueur de la série suivante"""
    courant = u[0]
    compteur = 1
    tc = [courant]
    k = 1
    n = len(u)
    while k < n:
        if u[k] != courant:
            tc.append(compteur)
            compteur = 1
            courant = u[k]
        else:
            compteur += 1
        k += 1
    tc.append(compteur)
    return tc

def decompresse(v):
    courant = v[0]
    u = [courant]*v[1]
    for k in range(2, len(v)):
        courant = 1 - courant
        u.extend([courant]*v[k])
    return u      

"""
In [3]: compresse([1, 1, 1, 0, 1, 0, 0, 1])
Out[3]: [1, 3, 1, 1, 2, 1]

In [4]: decompresse([1, 3, 1, 1, 2, 1])
Out[4]: [1, 1, 1, 0, 1, 0, 0, 1]
"""

Exercice 4 Suite diatomique de Stern

Citons Wikipedia :

Si l’on dispose la suite de Stern (en ommettant le premier terme 0) en lignes successives de 1, 2, 4, 8, … termes, comme dans la figure ci-dessous, il se présente des propriétés remarquables.

La somme des termes de chaque ligne est une puissance de 3.
Les maxima de chaque ligne constituent la suite de Fibonacci.
Si on omet le 1 initial, chaque ligne est un palindrome.
Chaque colonne forme une suite arithmétique. La suite formée des raisons est la suite de Stern elle-même. Cela signifie que la suite de Stern dispose d’une structure fractale.

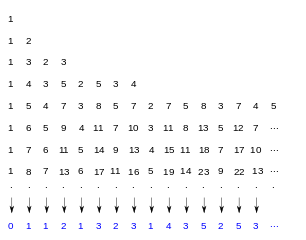
Crédits : Theon CC BY-SA

 

def suite_diatomique(n):
    t = [0] * (n + 1)
    t[0] = 0
    t[1] = 1
    for k in range(2, n, 2):
        t[k] = t[k // 2]
        t[k + 1] = t[k // 2] + t[k // 2 + 1]
    return t[-1]
    
def suite_diatomiqueV2(n):
    "voir https://fr.wikipedia.org/wiki/Suite_diatomique_de_Stern"
    if n == 0:
        return 0
    t = [1, 1]   #initialisation de t avec u(1) et u(2)
    indexmax = 2 #index du dernier terme de la suite  dans t
    while indexmax < n:
        indexmax = indexmax * 2
        t2 = []
        for k in range(len(t) - 1):
            t2.extend([t[k], t[k] + t[k+1]])
        t2.append(t[-1])
        t = t2
    return t[n - indexmax // 2]
    
def suite_diatomiqueV3(n):
    "avec fonction auxiliaire récursive et memoization dans un dictionnaire"

    def aux(n):
        if n in memo:
            return memo[n]
        elif n % 2 == 0:
            memo[n] = aux(n // 2)
            return memo[n]
        else:
            memo[n] = aux(n // 2) +  aux(n // 2 + 1)
            return memo[n]

    memo = {0 : 0, 1 : 1}
    return aux(n)
    
def suite_diatomiqueV4(n):
    decomposition = [n]
    terme = 0
    while len(decomposition) > 0:
        newdecomposition = []
        for m in decomposition:
            quotient, reste = m // 2, m % 2
            if reste == 0:
                if quotient == 1:
                    terme = terme + 1
                else:
                    newdecomposition.append(quotient)
            else:
                if quotient == 1:
                    terme = terme + 1
                    newdecomposition.append(quotient + 1)
                else:
                    newdecomposition.extend([quotient, quotient + 1])
        decomposition = newdecomposition
    return terme


# In [36]: [suite_diatomique(k) for k in range(10)]
# Out[36]: [0, 1, 1, 2, 1, 3, 2, 3, 1, 4]
  
# >>> suite_diatomique(10000001)
#9469

Exercice 5 Suite de Fibonaccci


def fibonachiffres(n):
    """Retourne le rang du premier terme de la suite de Fibonacci avec n chiffres"""
    fibo = [0, 1]
    rang = 0
    puissance10 = 10
    nbchiffres = 1
    while nbchiffres < n:
        rang = rang + 1
        fibo[0], fibo[1] = fibo[1], fibo[0] + fibo[1]
        if fibo[0] >= puissance10:
            nbchiffres = nbchiffres + 1
            puissance10 = puissance10 * 10
    return rang

# In [5]: fibonachiffres(2020)
# Out[5]: 9663

Exercice 6 Entiers palindromes


def nombre2chiffres(n, b):
    "Retourne la liste des chiffres en base b de n"
    t = []
    while n >= b:        
        t.append(n % b)
        n = n // b
    t.append(n)
    return t[::-1]
    
def  chiffres2nombre(chiffres, base = 10):
    "Avec l'algorithme d'Horner"
    nombre = 0
    for k in range(0, len(chiffres)):
        nombre = nombre * base + chiffres[k]
    return nombre

def palindrome(liste):
    n = len(liste)
    for k in range(n // 2):
        if liste[k] != liste[n - 1 - k]:
            return False
    return True
    
def somme_palindrome_dix_deux(bsup):
    "Retourne la somme des entiers < bsup et palindromes dans les bases 10 et 2"
    s = 0
    for n in range(1, bsup):
        if palindrome(nombre2chiffres(n, 10)) and palindrome(nombre2chiffres(n, 2)):
            s = s + n
    return s
    
# In [15]: somme_palindrome_dix_deux(10**7)
# Out[15]: 25846868

#Critère de divisibilité par 7

Exercice 7


def divisible7(n):
    """Retourne un booléen indiquant si n divisible par 7"""
    bleu = [0, 3, 6, 2, 5, 1, 4]
    noir = [(k + 1)%7 for k in range(7)]
    chiffres = nombre2chiffres(n, 10)
    nbchiffres = len(chiffres)
    sommet = 0
    for i in range(nbchiffres):
        c = chiffres[i]
        sommet = bleu[sommet]
        for j in range(c):
            sommet = noir[sommet]
    return sommet == 0

Les arêtes en trait plein relient les sommets étiquetés par les restes successifs de la division euclidienne d’un entier naturel par 7, lorsqu’on passe d’un entier au suivant en ajoutant 1.

Les arêtes en pointillées relient les sommets étiquetés par les restes successifs de la division euclidienne d’un entier naturel par 7, lorsqu’on passe d’un entier au suivant en multipliant par 10.

# In [20]: [(10 ** k) % 7 for k in range(7)]
# Out[20]: [1, 3, 2, 6, 4, 5, 1]

Soit un entier \(n\) donc la suite des chiffres en base dix est \(c_{1}c_{2}\ldots c_{k}\) par ordre décroissant des puissances de dix associées.

D’après l’algorithme d’Horner, \(n\) est le terme \(u_{k}\) de la suite définie par : \(u_{0}=0\) et \(u_{p+1}=10 \times u_{p} + c_{p + 1}\).

Démontrons la correction de la fonction divisible7

On considère l’invariant de boucle I(p)= “Après l’itération d’index \(p\), on se trouve sur le sommet étiqueté par le reste de la division euclidienne par 7 de \(u_{p}\)”
I(0) est vrai, l’invariant est vrai avant l’entrée dans la boucle (précondition).
Supposons que I(p) soit vrai, c’est-à-dire qu’on se trouve au sommet étiqueté par \(u_{p}\) modulo 7. Comme on a \(u_{p+1}=10 \times u_{p} + c_{p + 1}\), le parcours de la flèche en pointillés issue du sommet, nous amène au sommet étiqueté par \(10 \times u_{p}\) modulo 7. Le parcours de \(c_{p+1}\) flèches en traits pleins, nous amène ensuite au sommet étiqueté par \(10 \times u_{p} + c_{p+1}=u_{p+1}\) modulo 7. L’invariant est donc conservé.
De plus la boucle se termine car l’entier \(n\) comporte un nombre fini de chiffres. Par conservation de l’invariant, il est vrai en sortie de boucle (postcondition) ce qui prouve la correction de l’algorithme.

Exercice 9 : rendu de monnaie glouton


def rendu_monnaie_glouton(somme, systeme):
    """Retourne la décomposition de somme sous forme
    d'une liste de pieces choisies par les pièces de la liste  systeme."""
    #tri des pièces du systeme par ordre decroissant de valeurs
    systeme_copie = sorted(systeme, reverse = True)  
    rendu = []
    for idpiece in range(len(systeme_copie)):
        piece = systeme_copie[idpiece]
        while somme >= piece:
            somme = somme - piece
            rendu.append(piece)
    #postcondition
    assert somme == 0, "Rendu impossible"
    return rendu

# In [7]: rendu_monnaie_glouton(520, [1, 2, 5, 10, 20, 50, 100, 200])
# Out[7]: [200, 200, 100, 20]

#Crash le rendu de monnaie est impossible dans ce système
#alors qu'il existe une solution minimale : 10 + 10  + 10 + 10 + 5 + 2 + 2 + 2
# In [19]: rendu_monnaie_glouton(51, [2, 5, 10, 50, 100])
# ---------------------------------------------------------------------------
# AssertionError                            Traceback (most recent call last)
# <ipython-input-19-9108a4c669ac> in <module>
# ----> 1 rendu_monnaie_glouton(51, [2, 5, 10, 50, 100])
# 
# 
# AssertionError: Rendu impossible

Exercice 10 : complexité du rendu de monnaie glouton


import matplotlib.pyplot as plt
import numpy as np

systeme = [1, 2, 5, 10, 20, 50, 100, 200]
plt.figure(figsize = (15,15))
for i, bsup in enumerate([1000,10000,50000,100000]):
    plt.subplot(2,2,i + 1)
    les_sommes = np.arange(bsup + 1)
    les_rendus = [len(rendu_monnaie_glouton(somme, systeme)) for somme in les_sommes]
    plt.plot(les_sommes, les_rendus, label = 'Nombre de pièces')
    plt.ylabel('Nombre de pièces')
    plt.xlabel('Somme')
    plt.title('Somme maximale = {}'.format(bsup))
    plt.plot([0,bsup],[0, bsup // systeme[-1]],
            label =r'$y =\frac{\mathrm{somme}}{\mathrm{piece}_{max}}$')
    plt.legend(loc='lower right')
plt.savefig('complexite-glouton.pdf')
plt.show()

Exercice 11 : marche aléatoire et fougère de Barnsley

A propos de la fougère de Barnsley, on pourra consulter https://fr.wikipedia.org/wiki/Foug%C3%A8re_de_Barnsley.

from random import random

def f1(x, y):
    return (0, 0.16*y)

def f2(x, y):
    return (0.85*x + 0.04*y, -0.04*x + 0.85*y + 1.6)

def f3(x, y):
    return (0.2*x - 0.26*y, 0.23*x + 0.22*y + 1.6)

def f4(x, y):
    return (-0.15*x + 0.28*y, 0.26*x + 0.24*y + 0.44)

def choixfonction():
    alea = random()
    if alea < 0.01:
        return f1
    elif alea < 0.86:
        return f2
    elif alea < 0.93:
        return f3
    return f4

"""
In [16]: sum([1 for k in range(1000) if choixfonction().__name__ == 'f2' ])/1000
Out[16]: 0.851
"""

def marche_aleatoire(n):
    """Retourne les  couples de coordonnées des différents points du parcours
    lors d'une marche aléatoire de n pas"""
    (x, y) = (2 * random() - 1,2 * random() - 1)
    lesx = [x]
    lesy = [y]
    for k in range(n):
        (x, y) = choixfonction()(x, y)
        lesx.append(x)
        lesy.append(y)
    return lesx, lesy

def exo14():
    (lesx, lesy) = marche_aleatoire(10000)
    plt.axis('equal') #repère orthonormal
    plt.plot(lesx, lesy, 'k,') #affichage sous forme de pixels noirs
    plt.show()
    plt.savefig('marche1000.png')

Corrigé du TP de Révisions

Révisions sur les boucles, les tests, les fonctions, les listes

Exercice 1 Persistance d’un entier